Introduction
This document (notebook) discusses number theory properties and relationships of the integer 2026.
The integer 2026 is semiprime and a happy number, with 365 as one of its primitive roots. Although 2026 may not be particularly noteworthy in number theory, this provides a great excuse to create various elaborate visualizations that reveal some interesting aspects of the number.
The computations in this document are done with the Raku package “Math::NumberTheory”, [AAp1].
Setup
use Math::NumberTheory;
use Math::NumberTheory::Utilities;
use Data::Importers;
use Data::Translators;
use Data::TypeSystem;
use Graph;
use Graph::Classes;
use JavaScript::D3;
Notebook priming code:
#%javascript
require.config({
paths: {
d3: 'https://d3js.org/d3.v7.min'
}});
require(['d3'], function(d3) {
console.log(d3);
});
2026 Is a Happy Semiprime with Primitive Roots
First, 2026 is obviously not prime—it is divisible by 2—but dividing it by 2 gives a prime, 1013:
is-prime(2026 / 2)
# True
Hence, 2026 is a semiprime. The integer 1013 is not a Gaussian prime, though:
is-prime(1013, :gaussian-integers)
# False
A happy number is a number for which iteratively summing the squares of its digits eventually reaches 1 (e.g., 13 → 10 → 1).
Here is a check that 2026 is happy:
is-happy-number(2026)
# True
Here is the corresponding trail of digit-square sums:
is-happy-number(2026, :trail).tail.head(*-1).join(' → ')
# 2026 → 44 → 32 → 13 → 10 → 1
Not many years in this century are happy numbers:
(2000...2100).grep({ is-happy-number($_) })
# (2003 2008 2019 2026 2030 2036 2039 2062 2063 2080 2091 2093)
The decomposition of 2026 as 2 * 1013 means the multiplicative group modulo 2026 has primitive roots. A primitive root exists for an integer n if and only if n is 1, 2, 4, p^k, or 2 p^k, where p is an odd prime and k > 0.
We can check additional facts about 2026, such as whether it is “square-free”, among other properties. However, let us compare these with the feature-rich 2025 in the next section.
Comparison with 2025
Here is a side-by-side comparison of key number theory properties for 2025 and 2026.
| Property | 2025 | 2026 | Notes |
|---|---|---|---|
| Prime or Composite | Composite | Composite | Both non-prime. |
| Prime Factorization | 3⁴ × 5² (81 × 25) | 2 × 1013 | 2025 has repeated small primes; 2026 is a semiprime (product of two distinct primes). |
| Number of Divisors | 15 (highly composite for its size) | 4 (1, 2, 1013, 2026) | 2025 has many divisors; 2026 has very few. |
| Perfect Square | Yes (45² = 2025) | No | Major highlight for 2025—rare square year. |
| Sum of Cubes | Yes (1³ + 2³ + … + 9³ = (1 + … + 9)² = 2025) | No | Iconic property for 2025 (Nicomachus’s theorem). |
| Happy Number | No (process leads to cycle including 4) | Yes (repeated squared digit sums reach 1) | Key point for 2026—its main “happy” trait. |
| Harshad Number | Yes (divisible by 9) | No (not divisible by 10) | 2025 qualifies; 2026 does not. |
| Primitive Roots | No | Yes | This is a relatively rare property to have. |
| Other Notable Traits | – (20 + 25)² = 2025 – Sum of first 45 odd numbers – Deficient number – Many pattern-based representations | – Even number – Deficient number – Few special patterns | 2025 is packed with elegant properties; 2026 is more “plain” beyond being happy. |
| Overall “Interest” Level | Highly interesting—celebrated in math communities for squares, cubes, and patterns | Relatively uninteresting—basic semiprime with no standout geometric or sum properties | Reinforces blog’s angle. |
To summarize:
- 2025 stands out as a mathematically rich number, often highlighted in puzzles and articles for its perfect square status and connections to sums of cubes and odd numbers.
- 2026, in contrast, has fewer flashy properties — it’s a straightforward even semiprime — but it qualifies as a happy number and it has a primitive root.
Here is a computationally generated comparison table of most of the properties found in the table above:
#% html
my &divisors-count = { divisors($_).elems };
<is-prime is-composite divisors-count prime-omega euler-phi is-square-free is-happy-number is-harshad-number is-deficient-number primitive-root>.map({ %(sub => $_, '2025' => ::("&$_")(2025), '2026' => ::("&$_")(2026) ) })
==> to-html(field-names => ['sub', '2025', '2026'], align => 'left')
| sub | 2025 | 2026 |
|---|---|---|
| is-prime | False | False |
| is-composite | True | True |
| divisors-count | 15 | 4 |
| prime-omega | 6 | 2 |
| euler-phi | 1080 | 1012 |
| is-square-free | False | True |
| is-happy-number | False | True |
| is-harshad-number | True | False |
| is-deficient-number | True | True |
| primitive-root | (Any) | 3 |
Phi Number System
Digits of 2026 represented in the Phi number system:
my @res = phi-number-system(2026);
# [15 13 10 6 -6 -11 -16]
Verification:
@res.map({ ϕ ** $_ }).sum.round(10e-11);
# 2026
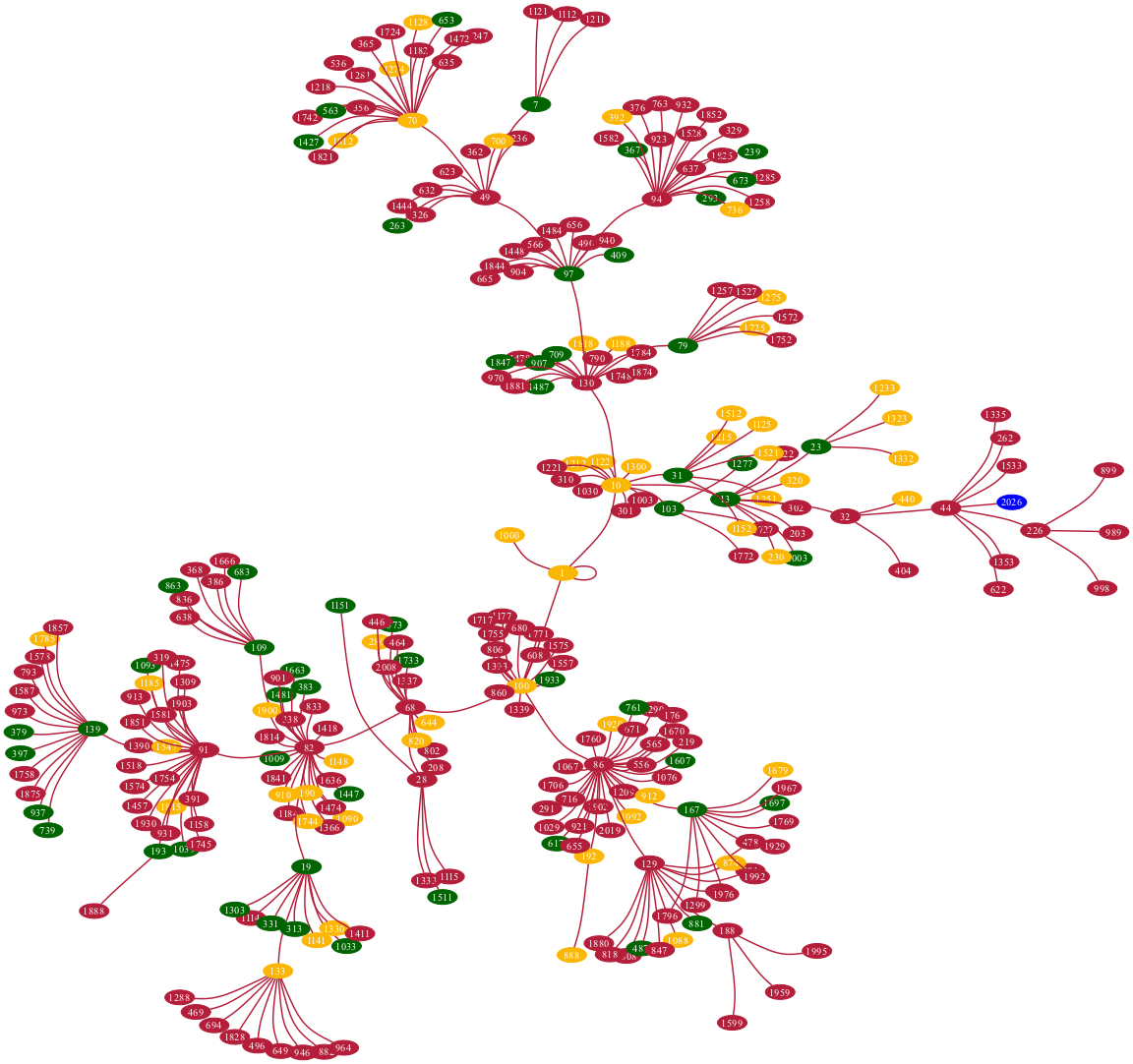
Happy Numbers Trail Graph
Let us create and plot a graph showing the trails of all happy numbers less than or equal to 2026. Below, we identify these numbers and their corresponding trails:
my @ns = 1...2026;
my @trails = @ns.map({ is-happy-number($_):trail }).grep(*.head);
deduce-type(@trails)
# Vector((Any), 302)
Here is the corresponding trails graph, highlighting the primes and happy numbers:
#% html
my @prime-too = @trails.grep(*.head).map(*.tail.head).grep(*.&is-prime);
my @happy-too = @ns.grep(*.&is-harshad-number).grep(*.&is-happy-number);
my %highlight = '#006400' => @prime-too».Str, # Deep Christmas green for primes
'Blue' => [2026.Str, ], # Blue for the special year
'#fbb606ff' => @happy-too».Str; # Darker gold for joyful numbers
my @edges = @trails.map({ $_.tail.head(*-1).rotor(2 => -1).map({ $_.head.Str => $_.tail.Str }) }).flat;
my $gTrails = Graph.new(@edges):!directed;
$gTrails.dot(
engine => 'neato',
graph-size => 12,
vertex-shape => 'ellipse', vertex-height => 0.2, vertex-width => 0.4,
:10vertex-font-size,
vertex-color => '#B41E3A',
vertex-fill-color => '#B41E3A',
arrowsize => 0.6,
edge-color => '#B41E3A',
edge-width => 1.4,
splines => 'curved',
:%highlight
):svg
Triangular Numbers
There is a theorem by Gauss stating that any integer can be represented as a sum of at most three triangular numbers. Instead of programming such an integer decomposition representation in Raku, we can simply use Wolfram|Alpha, [AA1, AA3], or wolframscript to find an “interesting” solution:
#% bash
wolframscript -code 'FindInstance[{2026 == PolygonalNumber[i] + PolygonalNumber[j] + PolygonalNumber[k], i > 10, j > 10, k > 10}, {i, j, k}, Integers]'
# {{i -> 11, j -> 19, k -> 59}}
Here, we verify the result using Raku:
say "Triangular numbers : ", <11 19 59>.&polygonal-number(:3sides);
say "Sum : ", <11 19 59>.&polygonal-number(:3sides).sum;
# Triangular numbers : (66 190 1770)
# Sum : 2026
Chord Diagrams
Here is the number of primitive roots of the multiplication group modulo 2026:
primitive-root-list(2026).elems
# 440
Here are chord plots [AA2, AAp1, AAp2, AAv1] corresponding to a few selected primitive roots:
#% js
my $n = 2026;
<339 365 1529>.map( -> $p {
my &f = -> $x { power-mod($p, $x, $n) => power-mod($p, $x + 1, $n) };
my @segments = circular-chords-tracing($n, with => &f, :d);
@segments .= map({ $_<group> = $_<group>.Str; $_ });
js-d3-list-line-plot(
@segments,
stroke-width => 0.1,
background => '#1F1F1F',
:300width, :300height,
:!axes,
:!legends,
:10margins,
color-scheme => 'Ivory',
#:$title-color, title => $p
)
}).join("\n")

Remark: It is interesting that 365 (the number of days in a common calendar year) is a primitive root of the multiplicative group generated by 2026. Not many years have this property this century; many do not have primitive roots at all.
(2000...2100).hyper(:4degree).grep({ 365 ∈ primitive-root-list($_) })
# (2003 2026 2039 2053 2063 2078 2089)
Quartic Graphs
The number 2026 appears in 18 results of the search “2026 graphs” in «The On-line Encyclopedia of Integer Sequences». Here is the first result (from 2025-12-17): A033483, “Number of disconnected 4-valent (or quartic) graphs with n nodes.” Below, we ingest the internal format of A033483’s page:
my $internal = data-import('https://oeis.org/A033483/internal', 'plaintext');
text-stats($internal)
# (chars => 2928 words => 383 lines => 98)
Here, we verify the title:
with $internal.match(/ '%' N (<-[%]>*)? <?before '%'> /) { $0.Str.trim }
# Number of disconnected 4-valent (or quartic) graphs with n nodes.
Here, we get the corresponding sequence:
my @seq = do with data-import('https://oeis.org/A033483/list', 'plaintext').match(/'[' (.*) ']'/) {
$0.Str.split(',')».trim
}
# [0 0 0 0 0 0 0 0 0 0 1 1 3 8 25 88 378 2026 13351 104595 930586 9124662 96699987 1095469608 13175272208 167460699184 2241578965849 31510542635443 464047929509794 7143991172244290 114749135506381940 1919658575933845129 33393712487076999918 603152722419661386031]
Here we find the position of 2026 in that sequence:
@seq.grep(2026):k
# (17)
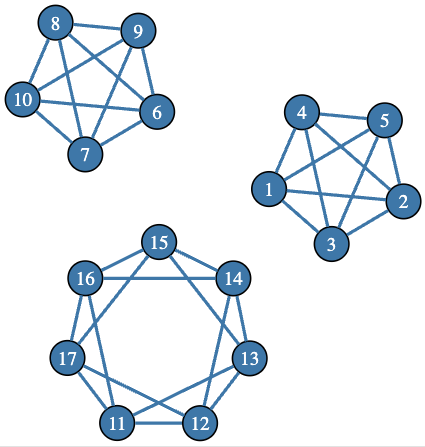
Given the title of the sequence and the extracted position of 2026, this means that the number of disconnected 4-regular graphs with 17 vertices is 2026. Let us create a few graphs from that set by using the 5-vertex complete graph (K₅) and circulant graphs.
Here is an example of such a graph:
#% html
reduce(
{ $^a.union($^b) },
[
Graph::Complete.new(5),
Graph::Complete.new(5).index-graph(6),
Graph::Circulant.new(7,[1,2]).index-graph(11)
]
).dot(engine => 'neato'):svg
And here is another one:
#% html
my $g = reduce(
{ $^a.union($^b) },
[
Graph::Complete.new(5).index-graph(13),
Graph::Circulant.new(12, [1, 5]).index-graph(1),
]
);
$g.dot(engine => 'neato', splines => 'curved'):svg
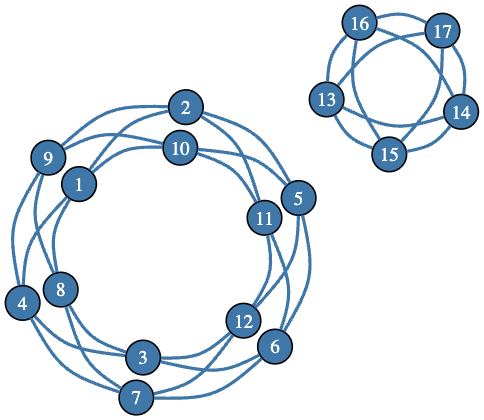
Here, we check that all vertices have degree 4:
$g.vertex-degree.sum / $g.vertex-count
# 4
Remark: Note that although the plots show disjoint graphs, each graph plot represents a single graph object.
Ways to compute 2026
Here are a few ways to compute 2026:
sub postfix:<!>(UInt:D $n) { [*] 1..$n }
[
2**11 - 22,
1 + 2 * 3 / 4 / 5 / 6 * 7! * 8 + 9,
1 + 2 + 3 * 4! + 5 / 6! * 7 * 8! - 9,
1 + 2 + 345 * 6 - 7 * 8 + 9,
1 - 2 * 3! * 456 * 7 + 8! + 9,
12 / 3! * 4**5 + 67 - 89,
12**3 + 45 / 6! * 7! - 8 - 9,
123 / 4! * 56 * 7 + 8 + 9,
9! / 8 / 7 / 6 + 5**4 + 321,
9 * 8 - 7 + 654 * 3 - 2 + 1,
987 + 6! + 5 * 4**3 - 2 + 1
]
# [2026 2026 2026 2026 2026 2026 2026 2026 2026 2026 2026]
Additional Comments
This section has a few additional (leftover) comments.
- After I researched and published the blog post “Numeric properties of 2025”, [AA1], in the first few days of 2025, I decided to program additional Number theory functionalities for Raku — see the package “Math::NumberTheory”, [AAp1].
- Most notably, “Math::NumberTheory” is extended to work with Gaussian integers, and the operators
GCDandLCDare also extended to work with rationals. - One of my current goals is to make Raku extremely good for researching Number theory phenomena.
- One of the most significant features of Raku is its bignum arithmetic and its good built-in numeric functions applicable in Number theory.
- Number theory provides many opportunities for visualizations, so I included utilities for some of the popular patterns in “Math::NumberTheory”, [AAp1, AAp2].
- I use the package “JavaScript::D3”, [AAp3], for almost all Number theory visualizations with Raku.
- Often, I visualize associated graphs using the DOT language specs provided by the package “Graph”, [AAp4] (as seen above).
- The Graphviz engines generate images in different formats using DOT specs.
- The number of years in this century that have primitive roots and have 365 as a primitive root is less than the number of years that are happy numbers.
- I would say I spent too much time finding a good, suitable, Christmas-themed combination of colors for the trails graph.
- To get the quartic graph counting sequence A033483, I tried to use “Math::Sequences”, but since that package does not provide the sequence, I used an ad hoc retrieval (for which Raku is perfect.)
- While working on this document, I implemented in “Math::NumberTheory” a set of new functions:
integer-digits,is-happy-number,is-harshad-number,is-abundant-number,is-perfect-number,is-deficient-number,abundant-number,deficient-number, andperfect-number.- All of these functions — except
integer-digits— had lower implementation priority.
- All of these functions — except
- Another implementation effort was to finally come up with a Command Line Interface (CLI).
- I advocate that a CLI should be considered for all Raku packages, and most should have one.
- I advocate that a CLI should be considered for all Raku packages, and most should have one.
#%bash
number-theory is happy number 2026
# True
#%bash
number-theory primitive root list 2026 | grep 365
# 365
References
Articles, blog posts
[AA1] Anton Antonov, “Numeric properties of 2025”, (2025), RakuForPrediction at WordPress.
[AA2] Anton Antonov, “Primitive roots generation trails”, (2025), MathematicaForPrediction at WordPress.
[AA3] Anton Antonov, “Chatbook New Magic Cells”, (2024), RakuForPrediction at WordPress.
[EW1] Eric W. Weisstein, “Quartic Graph”. From MathWorld–A Wolfram Resource.
Notebooks
[AAn1] Anton Antonov, “Primitive roots generation trails”, (2025), Wolfram Community. STAFFPICKS, April 9, 2025.
[EPn1] Ed Pegg, “Happy 2025 =1³+2³+3³+4³+5³+6³+7³+8³+9³!”, Wolfram Community, STAFFPICKS, December 30, 2024.
Packages, paclets
[AAp1] Anton Antonov, Math::NumberTheory, Raku package, (2025), GitHub/antononcube.
[AAp2] Anton Antonov,
NumberTheoryUtilities, Wolfram Language paclet, (2025), Wolfram Language Paclet Repository.
[AAp3] Anton Antonov, JavaScript::D3, Raku package, (2021-2025), GitHub/antononcube.
[AAp4] Anton Antonov, Graph, Raku package, (2024-2025), GitHub/antononcube.
Videos
[AAv1] Anton Antonov, Number theory neat examples in Raku (Set 3), (2025), YouTube/@AAA4prediction.

Related Wolfram Language notebooks / discussions:
LikeLike